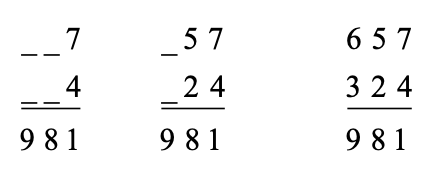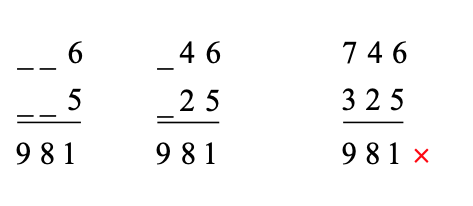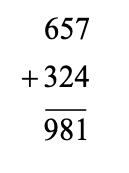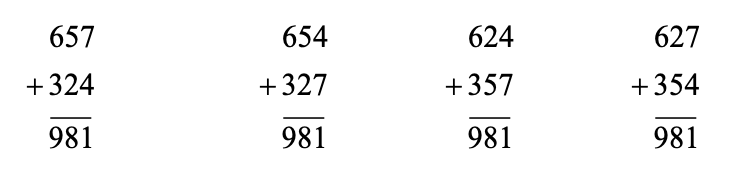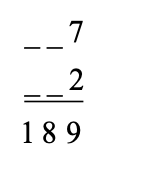LEARNING AND TEACHING

Learning Support at St Andrews

“The biggest mistake in teaching is to treat all children as if they were variants of the same individual and thus to feel justified in teaching them all the same subjects in the same way.”

Howard Gardner

For every behaviour, there is a reason. Our job in Learning Support is to aid parents and teachers to dig beneath the surface and help to identify what is going on for each student. It is to strategise and find out what works for each individual to assist their learning and development. Being able to identify what is going on for students early is important; early intervention is critical in helping children develop the necessary skills and strategies to enhance their development.

Strategies that work for one student, may not work for another:

“Even though students learn in many different ways, the essential skills and content they learn can remain steady. That is, students can take different roads to the same destination.”

Carol Ann Tomlinson

For the student with Autism Spectrum Disorder (ASD) they may struggle socially and find communication difficult. This may result in high levels of stress. People with ASD constantly strive to make sense of their environment, and the people and rules that govern it. These students need those around them to be:

• Consistent and predictable - provide timely warnings of any upcoming changes.
• Avoid emotion, appeal to their sense of logic.
• Use visuals.
• Limit choices.

Students with a Developmental Language Disorder find learning language challenging. It impacts their understanding of what people say to them, and often their ability to articulate their ideas and feelings. These students often struggle with vocabulary, grammar, sequencing and organisation to name a few.

Some strategies to support these students include:

• The gift of time to process.
• Use visual support materials.
• Use short, simple sentences when giving instructions or important information.
• Be clear and structured - provide simple written instructions for homework, assignments or tests.

Attention Deficit Hyperactivity Disorder (ADHD) is a complex disorder which affects a person’s ability to exert age-appropriate self-control. It is characterised by persistent and developmentally inappropriate patterns of behaviour, such as impulsivity or inattention. While it is common for everyone to occasionally be impulsive or inattentive, a person with ADHD will be more frequently challenged and more severely impaired by these behaviours. A person can have either inattentive or hyperactive tendencies, or in some cases they have both.

Strategies to support students:

• Provide clear expectations for behaviour.
• Provide predictable routines as much as possible.
• Provide clear, explicit instructions.
• Offer opportunities for movement, or body breaks.

For individuals with a Specific Learning Disorder, problems with reading, writing, spelling or Mathematics cannot be explained by low intellectual ability, by another disorder, a person’s lack of education, or a visual or hearing impairment.

A specific learning disorder affects how individuals learn in a variety of ways including how they take in, remember, understand or express information. A specific learning disorder may be defined as problems people encounter in learning that affect achievement.

There are a number of specific learning disorders:

Dyslexia – A specific learning disorder or disability in reading.

Dysgraphia – A specific learning disorder or disability in written expression

Dyscalculia – A specific learning disorder or disability in mathematics

Things that you can do to support a student with Dyslexia:

• Give me time to orally express my ideas but don’t expect that the quality of what I write will match what I can say.
• Provide an audio book.
• Mark my ideas, not my spelling.
• Let me take a photo of the board.

At St Andrews, we endeavour to support your child/ren in the way that best suits them and their individual learning needs. We want to meet them where they are, make connections to what they already know and to build their learning from there. If there are things that particularly work well for your child, or that don’t work for your child, please contact your child’s teacher/s to let them know. The more we understand your child the better equipped we are to support their learning in the best way possible. You can also go to the Learning Support Page on the Hub to access more information and strategies Learning Support Parent Page.

Next term we will be trialing the presence of a Speech Pathologist on site each Tuesday. They will be working with selected students with a focus on language skills (across the school) as well as some social skills (Secondary School only). If you feel that your child would benefit, you can email me, however, there are very limited places. There will be a cost to parents for this service.

The Learning Support Teachers:

• Shirley Gillie – Head of Learning Support   sgillie@standrews.vic.edu.au
• Wendy Punay – Learning Support Teacher – Primary   wpunay@standrews.vic.edu.au
• Kerryn Terrington – Learning Support Teacher – Secondary kterrington@standrews.vic.edu.au

Blessings

The Learning Support Teachers 

Working Mathematically

Recently, I have been reading some interesting articles on the critical connections between numeracy and mathematics.

Increasingly research is showing that life and work in the 21st century is requiring higher levels of mathematics and numeracy of its citizens. Numeracy and mathematics are intrinsically connected and both are needed in our ever changing, globalized and technological world (Tout, D. 2020, p. 2)

One of the key outcomes of a 2017 review of mathematics education is that the mathematics, or numeracy, related tasks that people undertake involve much more than basic arithmetic skills and straightforward procedural competence. Increasingly, numeracy now refers to the capability to use a range of mathematical and statistical knowledge and skills to solve problems in the real world for a purpose. Thus, to be considered numerate, it is expected that people will need to know some mathematics, and be able to apply that mathematics within a real-world context.

At St Andrews, we are committed to providing our students with the necessary knowledge, skills and opportunities to further develop their mathematical understanding so that they can make valuable contributions to society.

In the first newsletter, I posed the following problem:

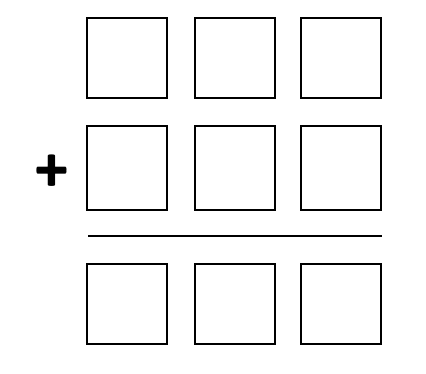
Task: 

a)   Take a piece of paper and tear it into nine squares. 

b)   Write the numbers from 1 to 9, one number on each square.

c)   Arrange the number tiles in the grid below so that the three-digit numbers formed make a correct addition. 

d)   Record any solutions you find

As promised, here is a solution to the problem:

Questions:

a)   How many solutions are there in total? Answer: 136

b)   How do you know that you have found them all? This is actually the most important aspect of the solution as it requires the most thinking and explanation.

After finding several different solutions, an important observation is that the sum of the digits in the “answer line” is 18. If you are interested in the formal proof of this, please contact me.

Considering that there will likely be many different combinations, creating an ordered list is an efficient strategy. In total there are 42 possible combinations of digits which sum to 18:

981, 972, 963, 954, 945, 936, 927, 918, 891, 873, 864, 846, 837, 819, 792, 783, 765, 756, 738, 729, 693, 684, 675, 657, 648, 639, 594, 576, 567, 549, 495, 486, 468, 459, 396, 387, 378, 369, 297, 279, 198, 189.

Testing the case of 981:

The only way to obtain a “1” in the “units” column is by having the two digits adding to 11. This is only possible with the combinations 9 and 2, 8 and 3, 7 and 4, 6 and 5.

As digits cannot be used twice, the combinations involving 9 and 8 are not possible.

Now, test the 7 and 4 option. The digits 1, 4, 7, 8 and 9 have been used. Therefore only 2, 3, 5 and 6 are available.

To fill the spaces in the “tens” column, we have one “ten” carried from the addition of the 7 and 4. Hence, we need the remaining two digits to add to 7. The only option which works is 5 and 2. This then leaves the 6 and 3 to fill the spaces in the “hundreds” column. Checking the addition reveals that this is a valid solution.

Now, test the 6 and 5 option. The digits 1, 5, 6, 8 and 9 have been used. Therefore only 2, 3, 4 and 7 are available.

To fill the spaces in the “tens” column, we have one “ten” carried from the addition of the 6 and 5. Hence, we need the remaining two digits to add to 7. The only option which works is 4 and 2. This then leaves the 7 and 3 to fill the spaces in the “hundreds” column. However, this leaves a result which is greater than 9. Hence, this is not a valid solution.

Hence, a solution for the case of 981 is:

We can also see that it is possible to obtain four solutions using this combination of digits.

Following this logic for each of the 42 combinations of digits, with four solutions for each combination, there would be a maximum of 168 solutions in total.

However, we need to consider if any of the 42 combinations of digits are not possible.

Considering the case of 189:

The only way to get the “9” in the “units” column is by having the following combinations: 8 and 1, 7 and 2, 6 and 3, 5 and 4

Now, 8 and 1 is not possible as digits can only be used once.

If it was 7 and 2, then the only digits remaining are: 3, 4, 5, 6. There is no way to arrange these to ensure a one in the “hundreds” column and resulting of an answer of 189.

The same is true if 6 and 3 or 5 and 5 are chosen.

The same logic can be used to discount each of the following: 396, 387, 378, 369, 297, 279, 198, 189

As such, there are 8 combinations from the original 42 which do not work.

Hence, there are a total of 34 combinations which do work and for each of these combinations there are four possible solutions.

Therefore, there are a total of 136 solutions.

Some of the solution strategies which have been employed in solving this question are: Creating ordered lists, Looking for patterns, Working backwards and Breaking the problem into manageable parts, to name a few. Were there other strategies that you used?

The work of a mathematician is never done as there are always more questions to ask. Can the same frame and digits be used to create subtraction problems? If so, how many solutions are there? How will you know when you have them all? How do they relate to the addition problem?

I hope that this problem has provided for some interesting discussions around the kitchen table and an appreciation that the answer is only one very small part of the experience in solving mathematical problems.

Michael Swanborough

Head of Learning and Teaching

Pentagon Triangles

For our next challenge, take a regular pentagon and cut it into three triangles along its diagonals.

a) Explore the ways in which different shapes can be made with the triangles. Record at least four different shapes. In how many ways can the same lengths be matched?

b) Can you make a triangle from two pieces? How? Record your result. Can you prove it?

c) Can you make a triangle from three pieces, four pieces, five pieces, six pieces…..?

d) Is there anything special about the shapes of the triangles you have found?

e) What else can you discover?

Michael Swanborough

Head of Learning and Teaching

Parenting Ideas

A recent article on the Parenting Ideas Website “That’s Leadership Thinking” has some great advice for parents to help their children develop a leadership mindset.

Helping tween and teen boys navigate the world is challenging parenting territory. It’s tempting to put off the conversations that we need to have because they seem too hard to initiate. Parenting expert Michael Grose shares communication strategies from popular boy champions to help you have the conversations you need to have. 

For more great ideas and articles to help you in your parenting journey, explore the Parenting Ideas website here.

Michael Swanborough

Head of Learning and Teaching