Learning & 

Teaching

Don't Forget to access Our Home Learning Portal for remote learning!

Click on the links below to go straight to your child's Home Learning Community page.

Maths Conversations at Home

(Adapted from Math for Love - Dan Finkel)

In recent times parents have found themselves having more maths conversations than they used to, but how can we ensure conversations at home and school give children a consistent message about how we learn Mathematics? The key is to make them as joyful and productive as possible.

Here are three guidelines for math conversations. Over the next few weeks I will break these down to help parents support their children's learning at home:

1. Start from where things make sense
2. Be curious
3. Keep it light and nonjudgmental

Start from where things make sense

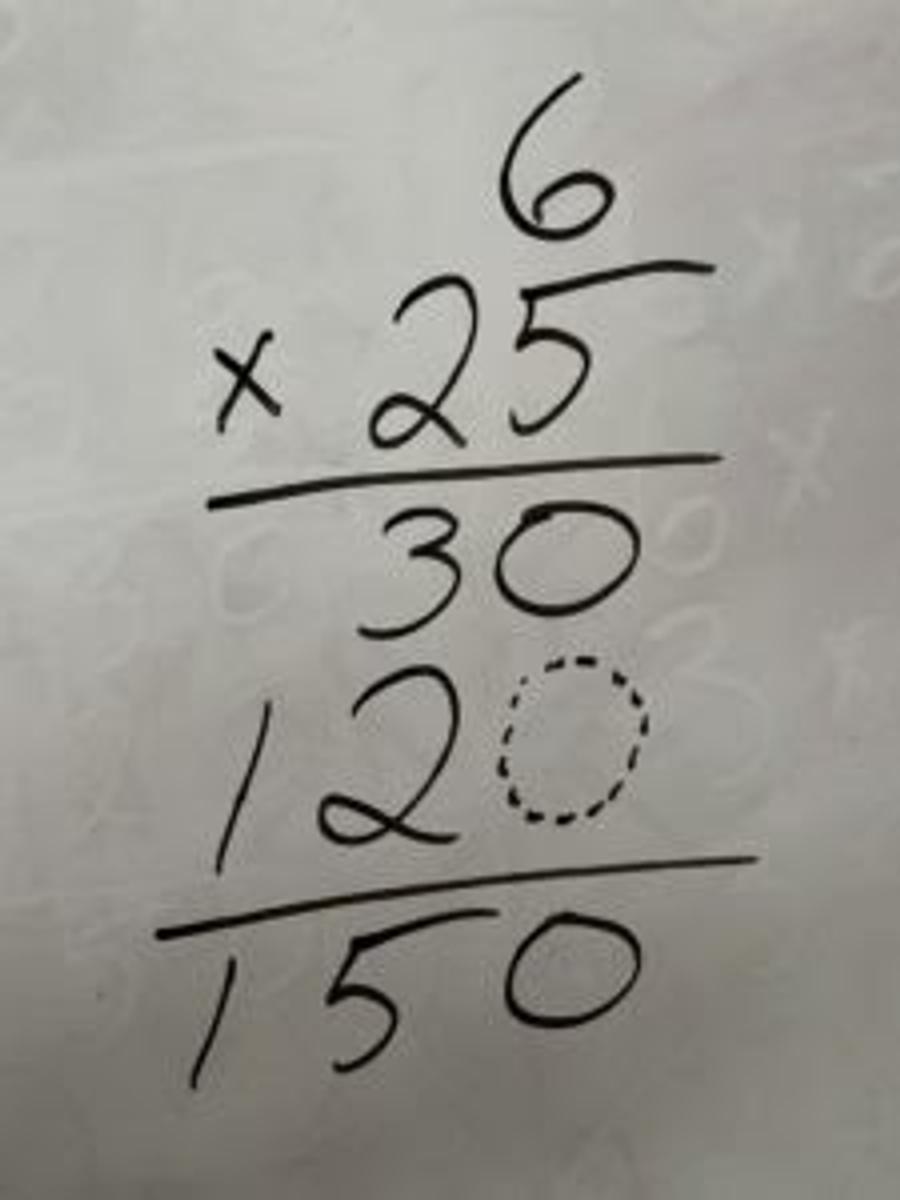
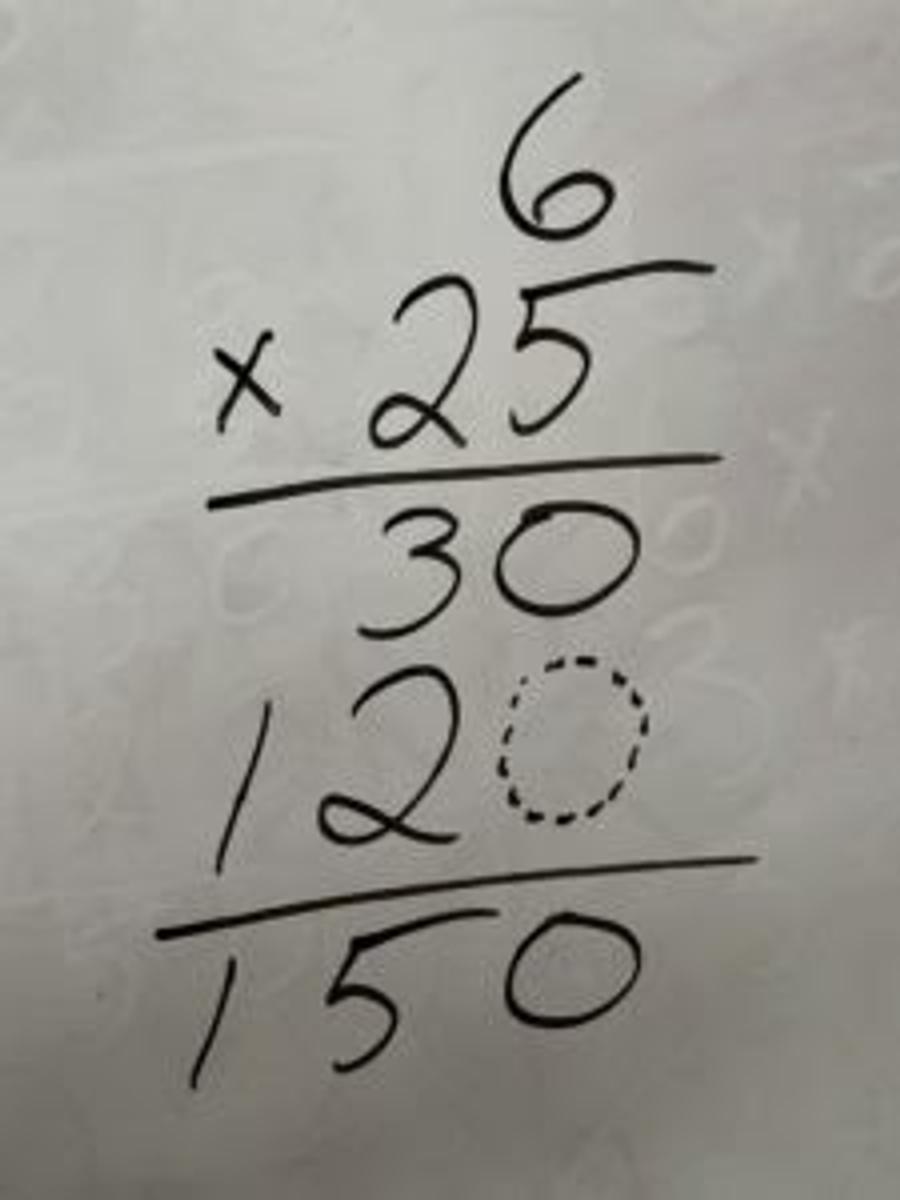
Let’s say you’re trying to solve 6 x 25 with your child. You want to help, so you show your child how you learned to solve the problem. So maybe you set it up vertically.

This gets you the right answer. But when you try to explain it to your child, you realise you don’t actually understand it. That 5 x 6 = 30 part makes sense to you, but the 2 x 6 = 12 part makes less sense. Why do you move that 12 over, and why do you write in (or not, depending on how you learned it) a ghost zero? The answer is right, so it works, but WHY does it work?

In his book Arithmetic, Paul Lockhart wrote “adults tend to confuse familiarity with understanding.” Arithmetic, like many ideas in maths, is powerful in part because it hides so much. So we need to steer toward understanding rather than saying “do it like this because that’s how I learned to do it.”

Some questions that move us toward understanding:

• I don’t understand why that works. Can you explain it to me?
• Why did you put the twelve there (or any specific point that doesn’t make sense)?
• What would a picture of that look like?

Drawing a picture is often the critical move. The ability to draw pictures, models, diagrams, etc. is a sign that you have a robust understanding built on things actually making sense. (Could you draw a picture of 6 x 25 yourself? What would you draw?)

Can’t draw a picture of 6 x 25? What about:

• 6 x 20?
• 6 x 10?
• 6 x 5?
• 3 x 5?
• 3 x 2?
• 3 x 1?

Maybe you feel silly for going back to such an easy problem. But mathematicians do this ALL the time. Go to an “easier case” and try to get a feel for what’s going on. Maybe you realise you don’t really understand what multiplication even means. But if you do, you should be able to draw a picture of 3 x 2 that illustrates it. For example:

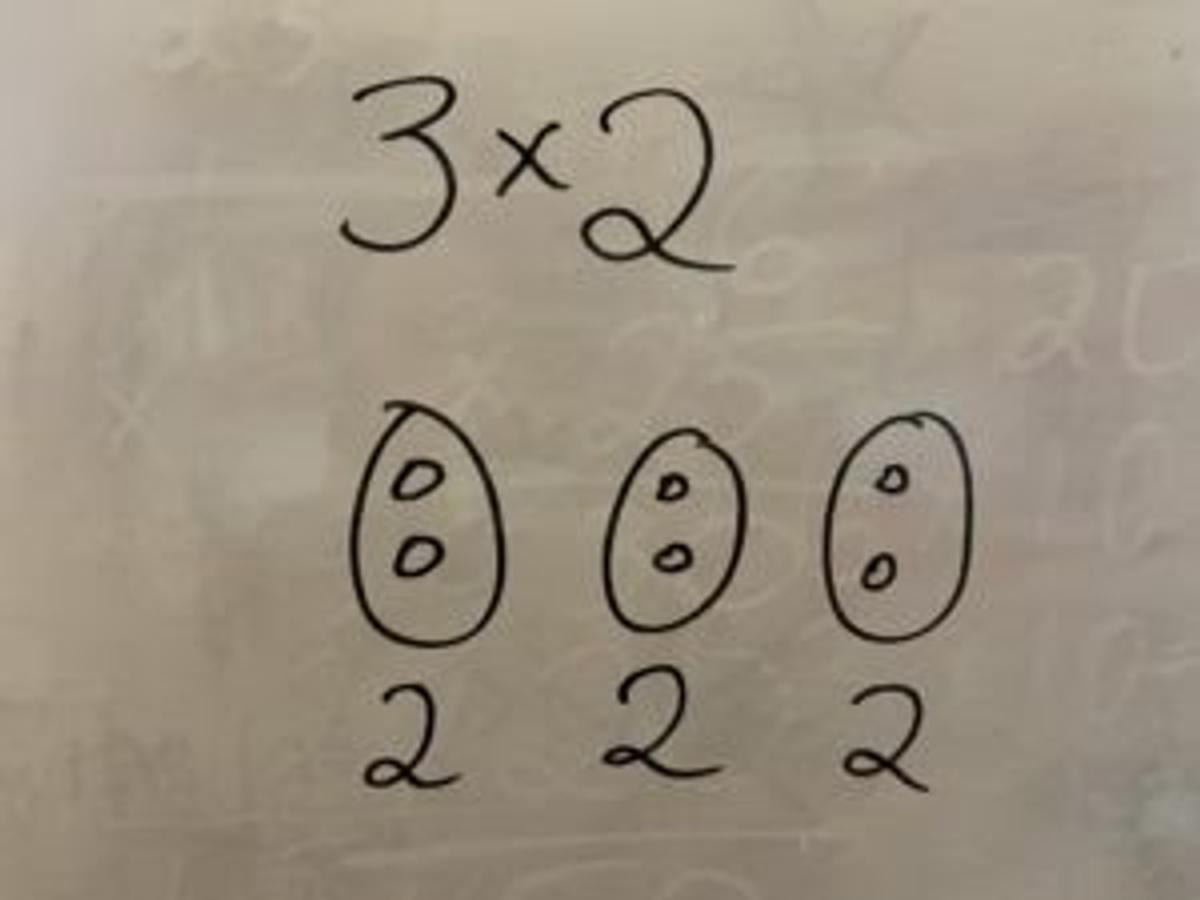
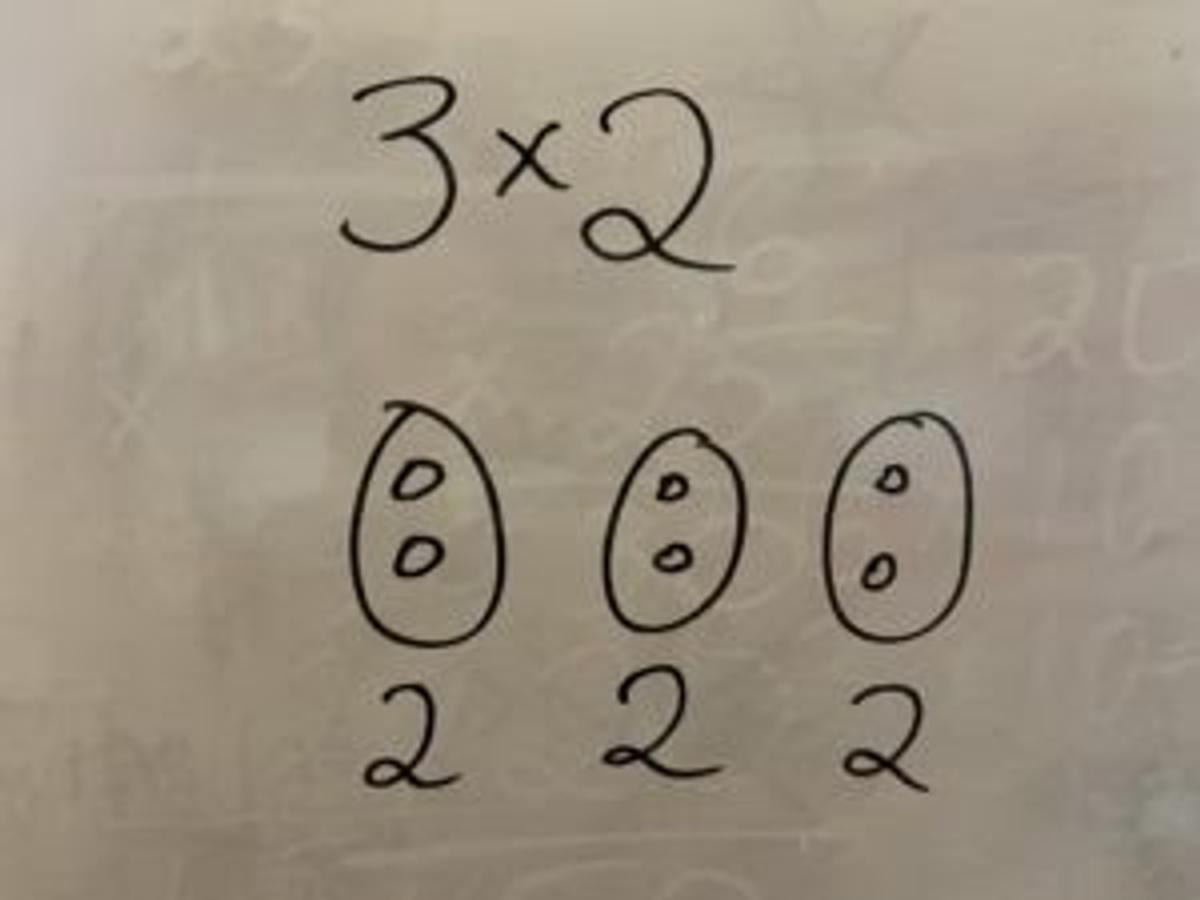
In this drawing, I’ve got 3 x 2 representing 3 GROUPS OF 2. Could I make a drawing of 3 x 5 then? Of 6 x 5? Of 6 x 10? Suddenly it doesn’t seem as hard. By making things simpler, you’ve actually created a ladder to climb down, and then to climb back up again!

Summary

If you are supporting your child’s Maths learning at home, I encourage you to make a habit of saying some variation of the statements below. 

Start from where things make sense

• “How could we draw a picture so this made sense?”
• “This feels confusing. Let’s start with an easier problem.”
 

Here’s to having productive and joyful math conversations at home!