Enrichment Mathematics Program

Enrichment Mathematics Program

Congratulations to Luca Emmerson (Year 5), Hugh Caton (Year 6), Akshat Dev (Year 7) and Angelo Dela Cruz (Year 8) who all took part in an Enrichment Program run by the Australian Mathematics Trust. During Terms 2 and 3 the boys worked on a series of questions from a program and were given mentoring by Miss Frost and could work through a text based on their program. Other than this support all questions had to be worked through individually and explanations of their working was always expected. The boys were given 8 to 12 very challenging questions from a range of contexts such as Logic, Geometry, Number Bases and applied Arithmetic problems.

Luca completed the Ramunajan Program with a perfect score and High Distinction, Hugh completed the Newton Program and gained a Distinction, Akshat completed the Dirichlet program with a perfect score and High Distinction as did Angelo in the Euler program, which was above his year level .

An example of part of questions asked is given below.

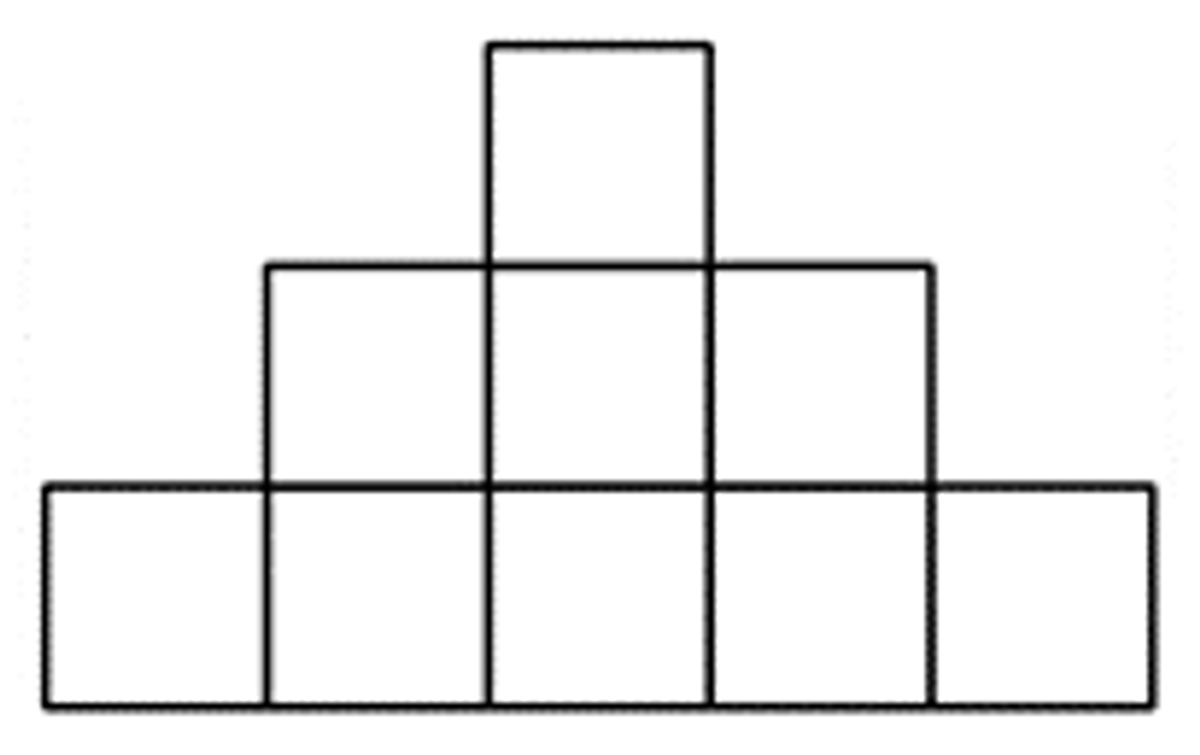
Ramanujan Program

How many rectangles can be drawn on this grid?

Remember squares are rectangles !

Newton Program 

Let x, y, z be digits so that the 9-digit number 5x36y98z2 is divisible by 792.

Without calculating x and y, explain why z=3 or 7.

Dirichlet Program

In base 13 the letters A, B , C represent the numbers ten, eleven, twelve respectively. Calculate 4C3B713 x A513 without converting to another base.

Euler Program

On his way from suburb A to suburb B, the bus driver maintained a speed of 44km/h. When he arrived at B, he found out that he needed to hurry to be back at A in time. So he drove the bus at a constant speed of 66km/h on his way back along the same route. At what constant speed could he have driven, there and back, so that the whole trip took the same time?

Miss Valerie Frost

Mathematics