La-on Canales Chun National Maths Summer School

Over the holidays, one of our high achieving Year 12 students, La-on Canales Chun attended the National Maths Summer School.  

The Northern Territory can only select one or two students a year to attend (in Canberra for 2 weeks over the summer holidays) and the last time we had someone participate was back in 2021 with Owen Chenhall.  

This is a very prestigious opportunity and La-on’s position was sponsored by the Maths Association of the NT who are very proud of him, as are his family and teachers. This is in addition to him also completing both Year 12 Maths last year (Specialist and Methods).

From La-on:

Thanks to the generous sponsorship from the MTANT, I was able to start this year off with an amazing experience that was the National Mathematics Summer School at the Australian National University from the 5th to the 18th of January. 

NMSS aims to bring passionate, eager young mathematicians from across the country to provide them with a taste of 'real' mathematics, outside of the school curriculum. I am extremely honoured to have had the opportunity to attend and represent the Northern Territory.

As one would assume at a maths school, the program was quite devoted to mathematics through lectures and periods of time dedicated to working on concepts learnt in such lectures called tutorials in the first half of the day. This was accompanied by an individual study session where tutors came into our rooms and aided us in whatever perplexing puzzle we were working on. 

Throughout the two-weeks, we were taught Number Theory first thing in the morning by the legendary Norman Do and Sean Gardiner. We started off with the idea of modular arithmetic, and the basic arithmetic operations in these new forms. This naturally led to axiomatic proofs, and the introduction of rings and isomorphisms. Euclid's algorithm was a recurring theme in this topic, which tied together with Diophantine equations and Pell's equation. The idea of a 'prime' number was built into every section of this course and allowed us to develop our understanding of what a prime actually was (and allowed us to try to come up with a definition on our own!).

We had two one-week courses, the first of which was Algorithms taught by Merryn Horrocks. Algorithms are the backbone of computer science (yet another discipline with a mathematical base). We started off with basic algorithms such as large summations and the idea of directing a brain-dead zombie to execute our computations. As we progressed, we started to search for optimised algorithms and were introduced to Turing Machines. Complexity theory was incredibly interesting and was about the behaviour of the time taken for an algorithm to execute a task with a very large number of steps. Although computational mathematics seemed wonderful, our final lecture was about the Entscheidungsproblem (decision problem) and the limits of computation.

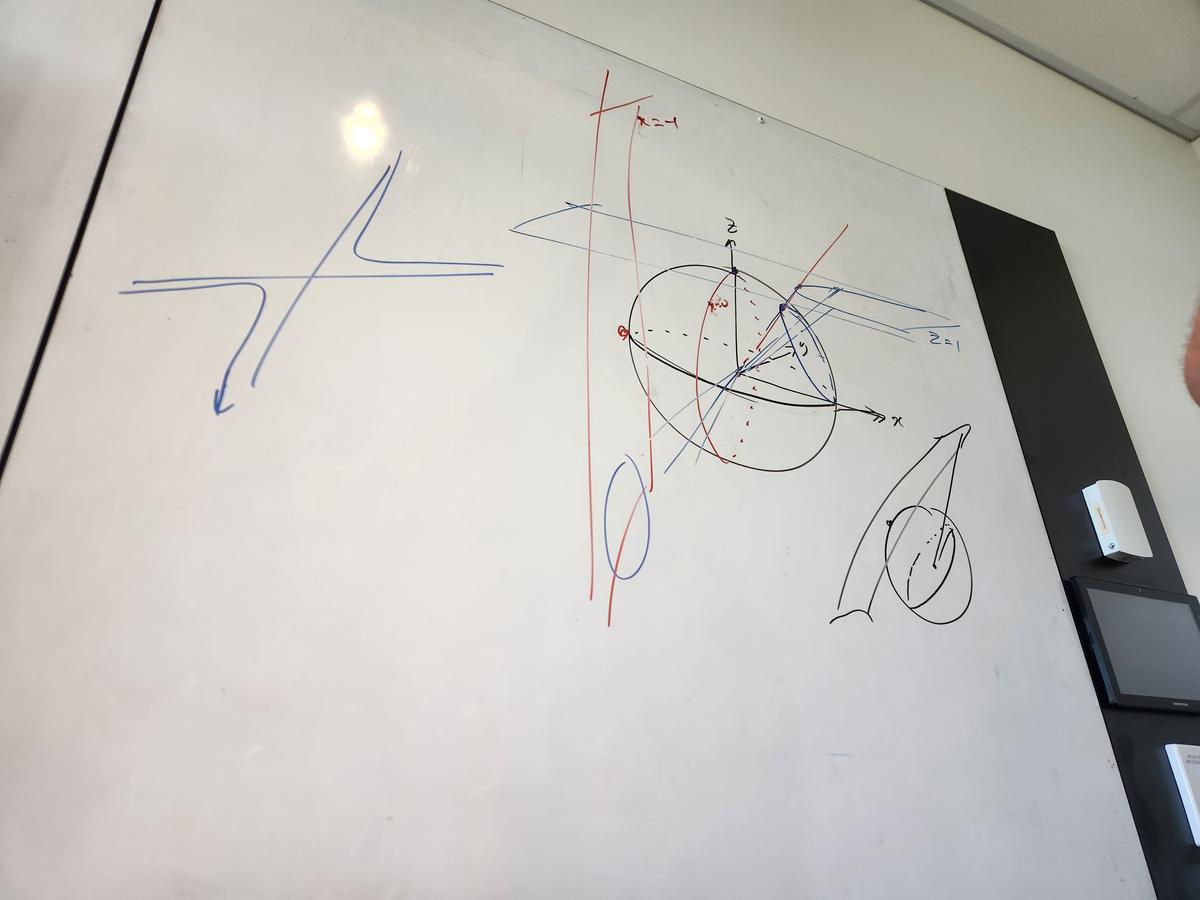
Our other one-week course was Flying Beyond the Plane (Projective Geometry) taught by Leanne Reynolds. I adored this topic. We explored the real projective plane (P2), which is an extension of our everyday real plane (R2). This extension includes points at infinity, which collectively form the line at infinity (pretty cool names!). There is no way to visualise P2, but we can represent it! My favourite representation is the spherical model which displays P2 as a sphere around the origin with a radius of 1, and the real plane touching the sphere at z=1. Any point on the real plane can have a line drawn through it to connect with the centre of the sphere. This intersects the sphere at some point called a homogenous coordinate. If we repeat this method for various conic sections, something beautiful happens; we can project a conic section into a different conic section! Below also shows a projection of a parabola into an ellipse, drawn by the incredible Zoltan Bacskai!

I truly loved projective geometry and hope to explore it further in other stages of my mathematical career!

Of course, the entirety of the school was not solely dedicated to mathematics, and there was time allocated for us to create friendships with each other via the common rooms, or expertly organised games. I met an amazing group of people from Sydney and surprisingly Tasmania, and I hope to stay in touch with them post-graduation. Halfway through the school, we had a maths relay in randomly allocated teams which was an incredibly high stakes, thrilling experience (even though my team didn't win). 

An excursion was held where we were able to visit different places in Canberra. I chose to visit the Museum and was shocked at the scale of relics held in one building. The school came to an end with the final concert and formal dinner. It is a truly beautiful finale to the hard work of many students and involved nearly all of us performing in some way whether it be through comedy, an act, music or juggling. I myself performed on the grand piano and in a poorly executed comedy skit with my friends!

Starting the year at NMSS was such an incredible, unforgettable experience. I am so happy to have been taught by passionate mathematicians, surrounded by more passionate young mathematicians, who all share my deep love for mathematics. I thank the MTANT for their generous sponsorship of which I assure that it was well spent. 

Finally, I would like to thank my truly legendary maths teacher, Ms Hutchinson for her support, and most importantly, showing me that NMSS existed. I genuinely encourage everyone with a passion in mathematics to go for it; I promise that you will not regret it.