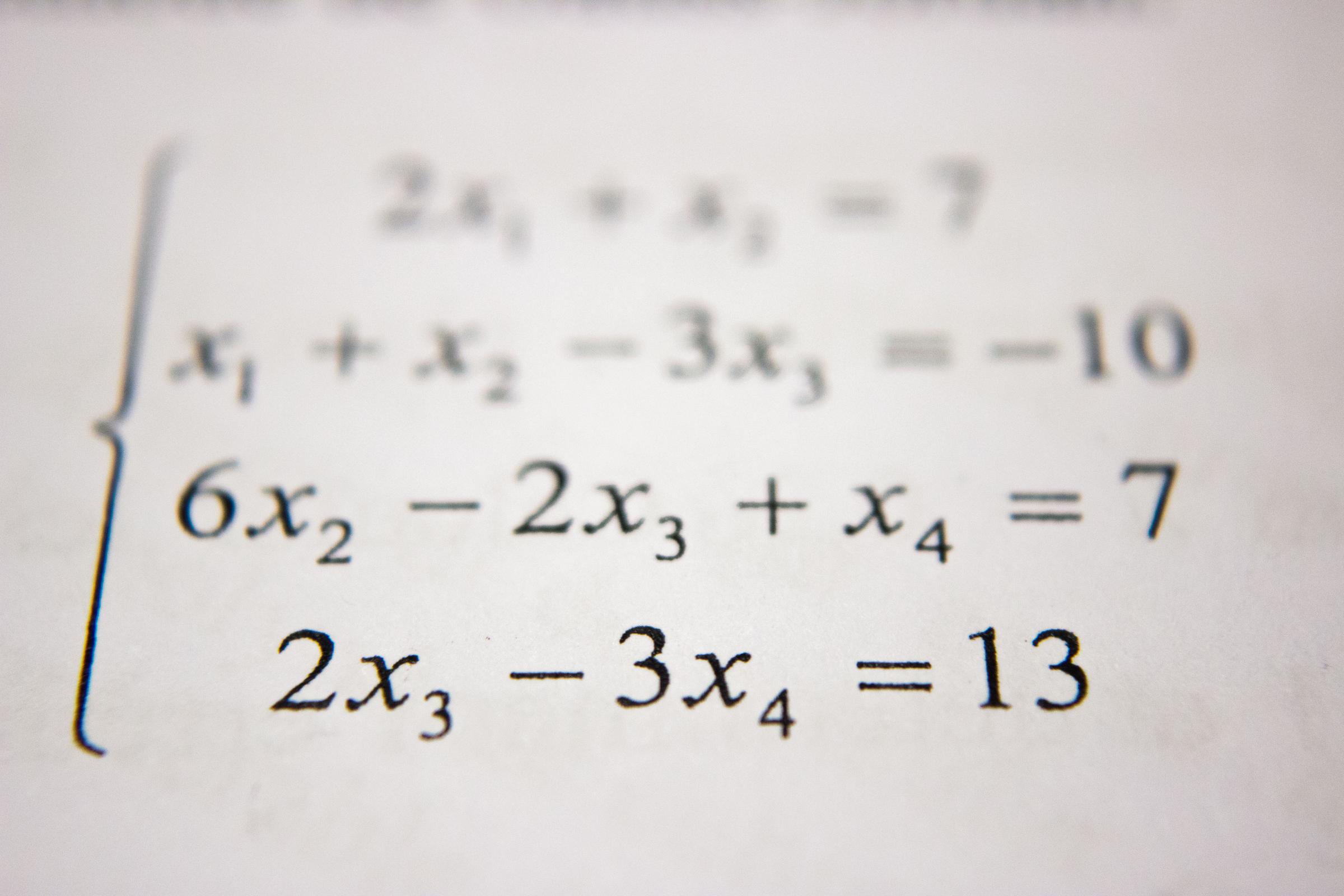
Numeracy improvement at BHHS
by Mr Greg Breese, Assistant Principal
At BHHS, we want all of our maths students to be improving their maths skills, learning collaboratively with other students, being challenged and experiencing success. Key beliefs that we foster in our students are “I can do maths”, “I’m getting better at maths”, and “Some maths problems need to be thought about for a while.” One of the school’s numeracy improvement strategies is the embedding of rich mathematical tasks into units of work. This draws on the work of Professor Peter Sullivan from Monash University.
Students explore rich mathematical tasks through a three-step process: Launch, Explore, Summarise. In the Launch step, the teacher introduces the problem to the students without telling them how to solve it. Students are enabled to think and talk about the mathematics of the problem.
In the Explore step, students investigate the problem and as they do apply their mathematical knowledge and skills to make sense of it. The teacher’s role is to observe the students and use questions to understand their thinking while also advancing them towards the learning goal of the lesson. Students may be required to struggle with the problem before making progress.
In the Summarise step, the teacher draws on student solutions they have observed to showcase methods for approaching the problem and uses a class discussion to have students reflect on the relatively strengths of these approaches. Exploring rich tasks in this way is intended to support students to develop resilience when faced with problems they do not immediately know the method for and to understand that maths problems can often be solved in more than one way, but often not all methods are equally effective. Students put themselves in the role of mathematicians, placing themselves not as recipients of mathematical knowledge but as participants in the mathematical community.
An example of a rich problem students might consider after studying square numbers is included below.
Look at the following row of numbers:
10, 15, 21, 4, 5
They are arranged so that each pair of adjacent numbers adds up to a square number: 10+15=25 15+21=36 21+4=25 4+5=9
Can you arrange the numbers 1 to 17 in a row in the same way, so that each adjacent pair adds up to a square number?
Can you arrange them in more than one way? If not, can you justify that your solution is unique?
Could you arrange larger sets of numbers in this way?