Building Mathematical Understanding

One of the things modern maths teachers hear the most from parents and carers is that maths is no longer taught in the way they learned it at school. Gone are the days of memorising number facts by rote - I have spoken about teaching for understanding in maths a few times earlier this year. Today I wanted to share a bit more information with you all about one of the ways we achieve this. 

Our approach to teaching maths is informed by a range of evidence-based research, one of which is the pedagogy of Concrete - Representational - Abstract (CRA), which is based on Jermone Brunner’s theory of cognitive development. Brunner was part of the Constructivist gang who believed that knowledge is built layer upon layer, with the integrity of each layer depending on the layer that preceded it. Brunner described the process through which humans build an internal view of the external world starting with enactive (action-based), moving through iconic (image-based) and finishing at symbolic (language-based). Typically speaking, when we learn a new concept we learn best by starting with actions that we can interact with before trying to represent that learning in pictures and then thinking about the concept abstractly. This learning is not linear and as the concepts we develop grow in complexity, it is often necessary to revisit earlier stages of learning multiple times to gain full understanding.

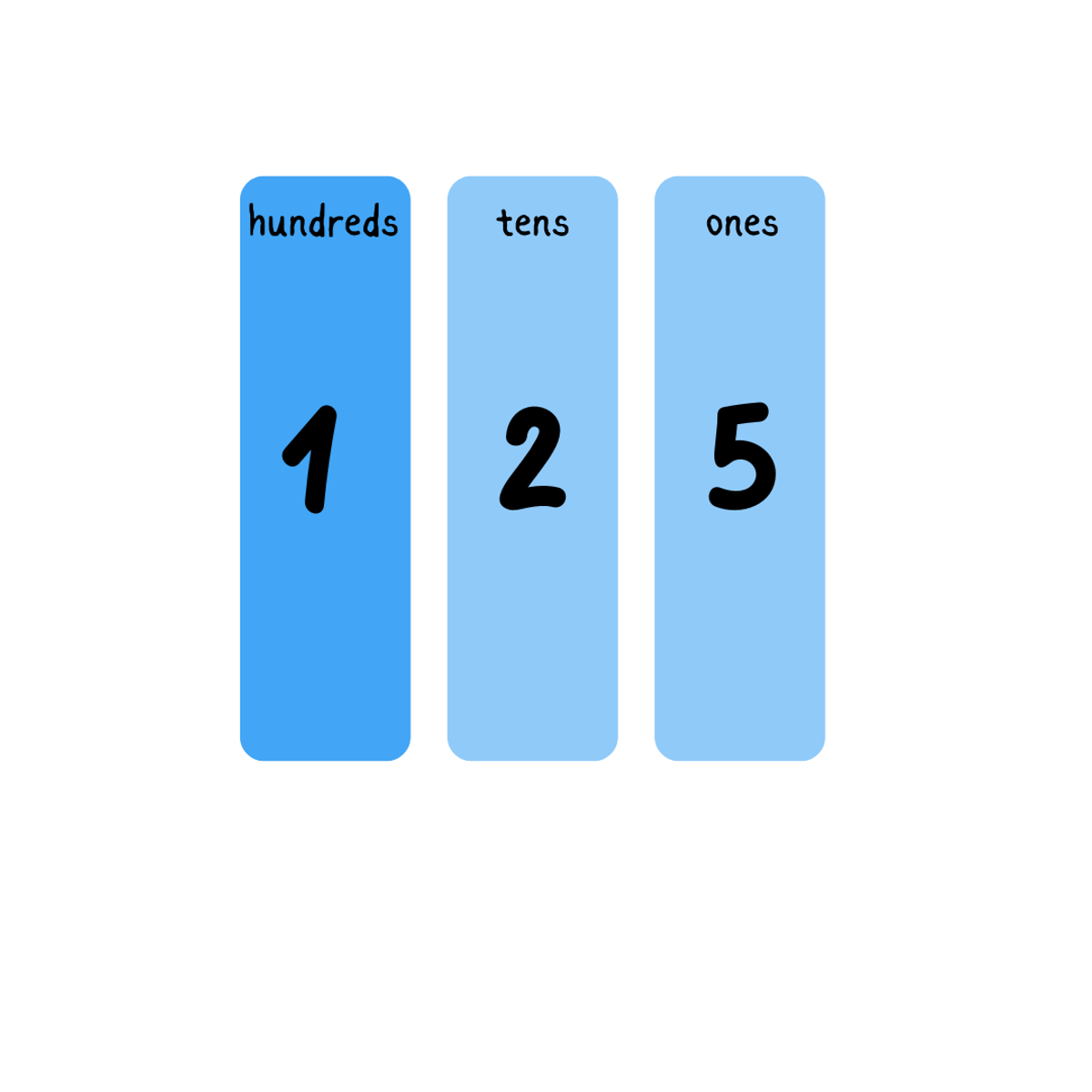
What this looks like in a maths classroom varies depending on the age of the learner, the concept being taught and their prior understandings. The concrete stage of a Foundation classroom may look like role play, with learners acting out situations and tracking the mathematical concept. In the Junior years, we might see what we call ‘concrete materials’ such as their fingers or counters, by the Middle grades we might see MAB (wooden representations of numbers at different place values) while Senior grades may see fraction pieces. Each of these experiences are concrete and moveable, but they also have abstract characteristics as the learners get older and have more mathematical concepts well established.

The representational stage of learning again will vary depending on the stage of the learner. In Foundation, our students may need detailed pictures of the characters in their mathematical stories, Junior students may be ready to display each number they are working with as a collection of dots or dashes on their page, our Middle students may start to represent the place value of numbers of MAB through dots, lines and squares while our Senior students might start to feel comfortable drawing a fraction of a shape.

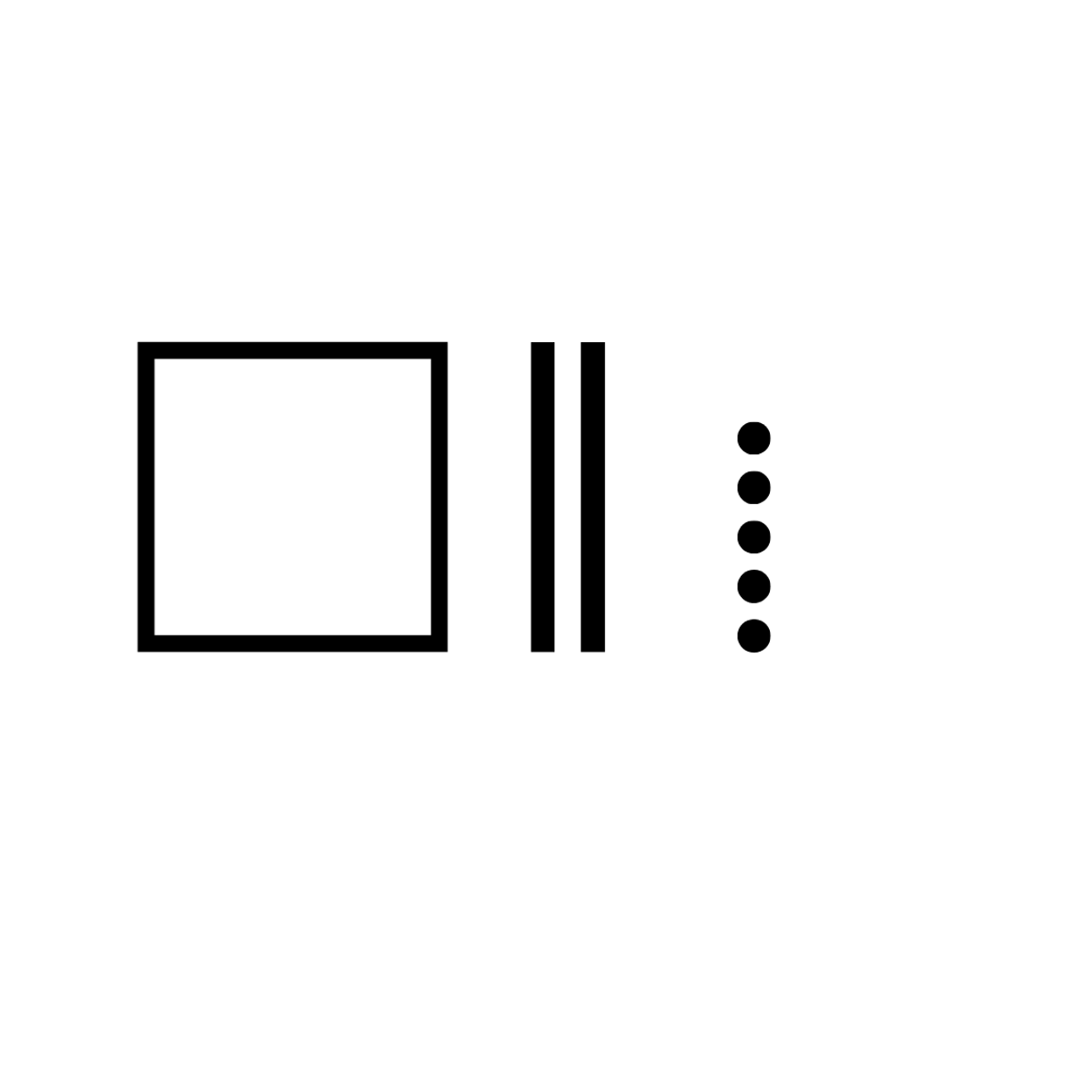
Finally we reach the abstract stage of learning. This is where our students start to use numbers and algorithms to represent the numbers and operations they are working with. 

We know that the psychology of a maths classroom is important for teachers and educators to remain aware of. 

Often students are keen to speed past (if not skip entirely) the concrete stage of learning; sometimes this is related to age (“I’m too old for counters - they are for the little kids”), sometimes it is related to perceived status (“Only kids who need extra help need to use concrete materials.”) The message from us is always that it is important to use the tools you require to understand! By skipping past the concrete stage too quickly, learners can lose opportunities for deep understanding, building connections and self-directed exploration that may impact their learning later on. I also like to point out that mathematicians at very high levels such as universities still pull out mathematical models and images when they need it!

And if you’ve got three spare minutes after reading this article and want to have a little chuckle, I recommend watching this video where Ma & Pa Kettle demonstrate just why mathematical understanding is just so important (apologies for the image quality)