Mathematics

Extension Maths Group Travels the Country
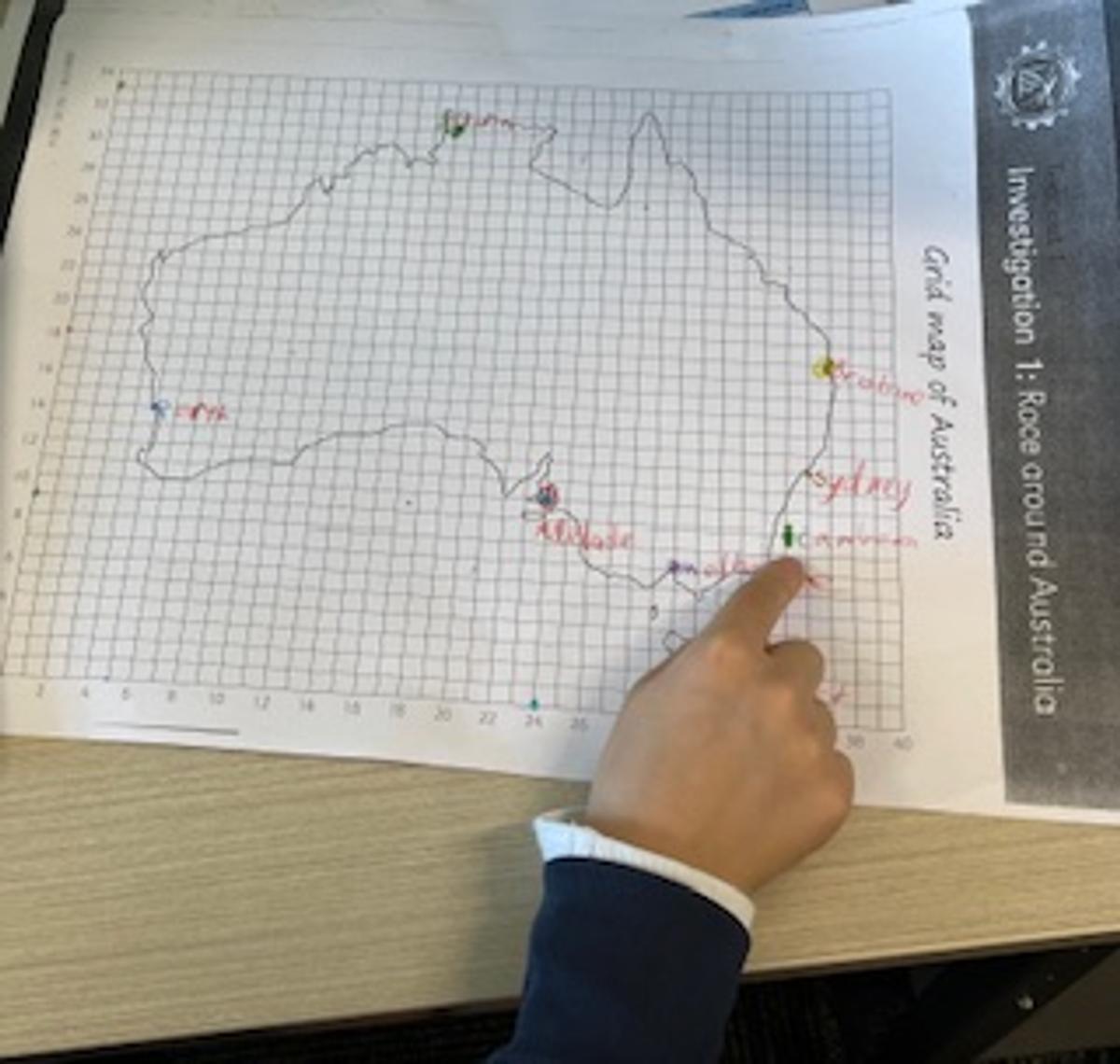
The Year 2 and 3 maths extension group is working out if it is possible to fly around Australia through all the capital cities in less than 24 hours. They had a lot of fun and really stretched their brains. Their verdict, possible or not, probably not recommended as a holiday plan.
The Victorian Curriculum - Mathematics
The Victorian Curriculum F–10 sets out what every student should learn during their first eleven years of schooling. The curriculum is the common set of knowledge and skills required by students for life-long learning, social development and active and informed citizenship.
The Victorian Curriculum F–10 incorporates the Australian Curriculum and reflects Victorian priorities and standards.
The Victorian Curriculum Assessment Authority (VCAA) published the Victorian Curriculum F–10 Version 2.0 Mathematics (Mathematics Version 2.0) in July 2023. All Victorian government and Catholic schools are now required to implement Mathematics Version 2.0 Foundation to Level 10A.
Rationale
Mathematics provides students with access to important mathematical ideas, knowledge and skills that they will draw on in their personal and work lives. The curriculum also provides students, as life-long learners, with the basis on which further study and research in mathematics and applications in many other fields are built.
Mathematical ideas have evolved across societies and cultures over thousands of years, and are constantly developing. Digital technologies are facilitating this expansion of ideas and provide new tools for mathematical exploration and invention. While the usefulness of mathematics for modelling and problem solving is well known, mathematics also has a fundamental role in both enabling and sustaining cultural, social, economic and technological advances and empowering individuals to become critical citizens.
Number, measurement and geometry, statistics and probability are common aspects of most people’s mathematical experience in everyday personal, study and work situations. Equally important are the essential roles that algebra, functions and relations, logic, mathematical structure and working mathematically play in people’s understanding of the natural and human worlds, and the interaction between them.
The Mathematics curriculum focuses on developing increasingly sophisticated and refined mathematical understanding, fluency, reasoning, modelling and problem-solving. These capabilities enable students to respond to familiar and unfamiliar situations by employing mathematics to make informed decisions and solve problems efficiently.
The curriculum ensures that the links between the various components of mathematics, as well as the relationship between mathematics and other disciplines, are made clear. Mathematics is composed of multiple but interrelated and interdependent concepts and structures which students apply beyond the mathematics classroom. For example, in Science, understanding sources of error and their impact on the confidence of conclusions is vital; in Geography, interpretation of data underpins the study of human populations and their physical environments; in History, students need to be able to imagine timelines and time frames to reconcile related events; and in English, deriving quantitative, logical and spatial information is an important aspect of making meaning of texts.
Aims
The Mathematics curriculum aims to ensure that students:
- develop useful mathematical and numeracy skills for everyday life, work and as active and critical citizens in a technological world
- see connections and apply mathematical concepts, skills and processes to pose and solve problems in mathematics and in other disciplines and contexts
- acquire specialist knowledge and skills in mathematics that provide for further study in the discipline
- appreciate mathematics as a discipline – its history, ideas, problems and applications, aesthetics and philosophy.
Structure
The curriculum is organised by the three strands of Number and Algebra, Measurement and Geometry, and Statistics and Probability.
Each strand is organised by sub-strands. Sub-strands group content descriptions under an appropriate concept, to provide both a focus and a clear sequence for the development of related concepts and skills within strands and across levels.
| Strands | Number and Algebra | Measurement and Geometry | Statistics and Probability |
|---|---|---|---|
| Sub-strands | Number and place value | Using units of measurement | Chance |
| Fractions and decimals | Shape | Data representation and interpretation | |
| Real numbers | Geometric reasoning | ||
| Money and financial mathematics | Location and transformation | ||
| Patterns and algebra | Pythagoras and trigonometry | ||
| Linear and non-linear relationships |
Number and Algebra
Number and Algebra are developed together, and each enriches the study of the other. Students apply number sense and strategies for counting and representing numbers. They explore the magnitude and properties of numbers. They apply a range of strategies for computation and understand the connections between operations. They recognise patterns and understand the concepts of variable and function. They build on their understanding of the number system to describe relationships and formulate generalisations. They recognise equivalence and solve equations and inequalities. They apply their number and algebra skills to conduct investigations, solve problems and communicate their reasoning.
Measurement and Geometry
Measurement and Geometry are presented together to emphasise their relationship to each other, enhancing their practical relevance. Students develop an increasingly sophisticated understanding of size, shape, relative position and movement of two-dimensional figures in the plane and three-dimensional objects in space. They investigate properties and apply their understanding of them to define, compare and construct figures and objects. They learn to develop geometric arguments. They make meaningful measurements of quantities, choosing appropriate metric units of measurement. They build an understanding of the connections between units and calculate derived measures such as area, speed and density.
Statistics and Probability
Statistics and Probability develops initially in parallel, with the curriculum progressively building links between them. Students recognise and analyse data and draw inferences. They represent, summarise and interpret data and undertake purposeful investigations involving the collection and interpretation of data. Students recognise variation, assess likelihood and assign probabilities using experimental and theoretical approaches. They develop an increasingly sophisticated ability to critically evaluate chance and data concepts and make reasoned judgments and decisions, as well as building skills to critically evaluate statistical information and develop intuitions about data.
Achievement standards
In Mathematics, students progress along a curriculum continuum that provides the first achievement standard at Foundation and then at Levels 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10. Level 10 also has an optional Level 10A, which is intended for students requiring further mathematical studies.
A 'Towards Foundation Levels A to D' curriculum is provided for students with disabilities or additional learning needs in this curriculum area.
Learning in Mathematics
The proficiencies of Understanding, Fluency, Problem Solving and Reasoning are fundamental to learning mathematics and working mathematically and are applied across all three strands Number and Algebra, Measurement and Geometry, and Statistics and Probability.
Understanding refers to students building a robust knowledge of adaptable and transferable mathematical concepts and structures. Students make connections between related concepts and progressively apply the familiar to develop new ideas. They develop an understanding of the relationship between the ‘why’ and the ‘how’ of mathematics. Students build understanding when they:
- connect related ideas
- represent concepts in different ways
- identify commonalities and differences between aspects of content
- describe their thinking mathematically
- interpret mathematical information.
Fluency describes students developing skills in choosing appropriate procedures, carrying out procedures flexibly, accurately, efficiently and appropriately, and recalling factual knowledge and concepts readily. Students are fluent when they:
- make reasonable estimates
- calculate answers efficiently
- recognise robust ways of answering questions
- choose appropriate methods and approximations
- recall definitions and regularly use facts,
- can manipulate expressions and equations to find solutions.
Problem-solving is the ability of students to make choices, interpret, formulate, model and investigate problem situations, select and use technological functions and communicate solutions effectively. Students pose and solve problems when they:
- use mathematics to represent unfamiliar or meaningful situations
- design investigations and plan their approaches
- apply their existing strategies to seek solutions
- verify that their answers are reasonable.
Reasoning refers to students developing an increasingly sophisticated capacity for logical, statistical and probabilistic thinking and actions, such as conjecturing, hypothesising, analysing, proving, evaluating, explaining, inferring, justifying, refuting, abstracting and generalising. Students are reasoning mathematically when they:
- explain their thinking
- deduce and justify strategies used and conclusions reached
- adapt the known to the unknown
- transfer learning from one context to another
- prove that something is true or false
- make inferences about data or the likelihood of events
- compare and contrast related ideas and explain their choices.
Information Communication Technologies and Mathematics
Information Communication Technologies (ICT) are powerful tools that can support student learning. Students can develop and demonstrate their understanding of concepts and content in Mathematics using a range of ICT tools. It is also important that students know how to use these ICT efficiently and responsibly, as well as learning how to protect themselves and secure their data.
If you have any questions about Mathematics at St Cecilia's please contact:
Kate Sutherland, Mathematics Leader
ksutherland@scgleniris.catholic.edu.au