Mathematics overview

Mathematics is the study of function and pattern in number, logic, space and structure. It provides both a framework for thinking and a means of symbolic communication that is powerful, logical, concise and precise. It also provides a means by which people can understand and manage their environment. Essential mathematical activities include calculating and computing, abstracting, conjecturing, proving, applying, investigating, modelling, and problem posing and solving.
This study is designed to provide access to worthwhile and challenging mathematical learning in a way which takes into account the needs and aspirations of a wide range of students. It is also designed to promote students’ awareness of the importance of mathematics in everyday life in a technological society, and confidence in making effective use of mathematical ideas, techniques and processes.
MGSC offers a range of Mathematics courses to suit different abilities and all career paths. We also include access to ICT resources/applications to facilitate the required learning outcomes.
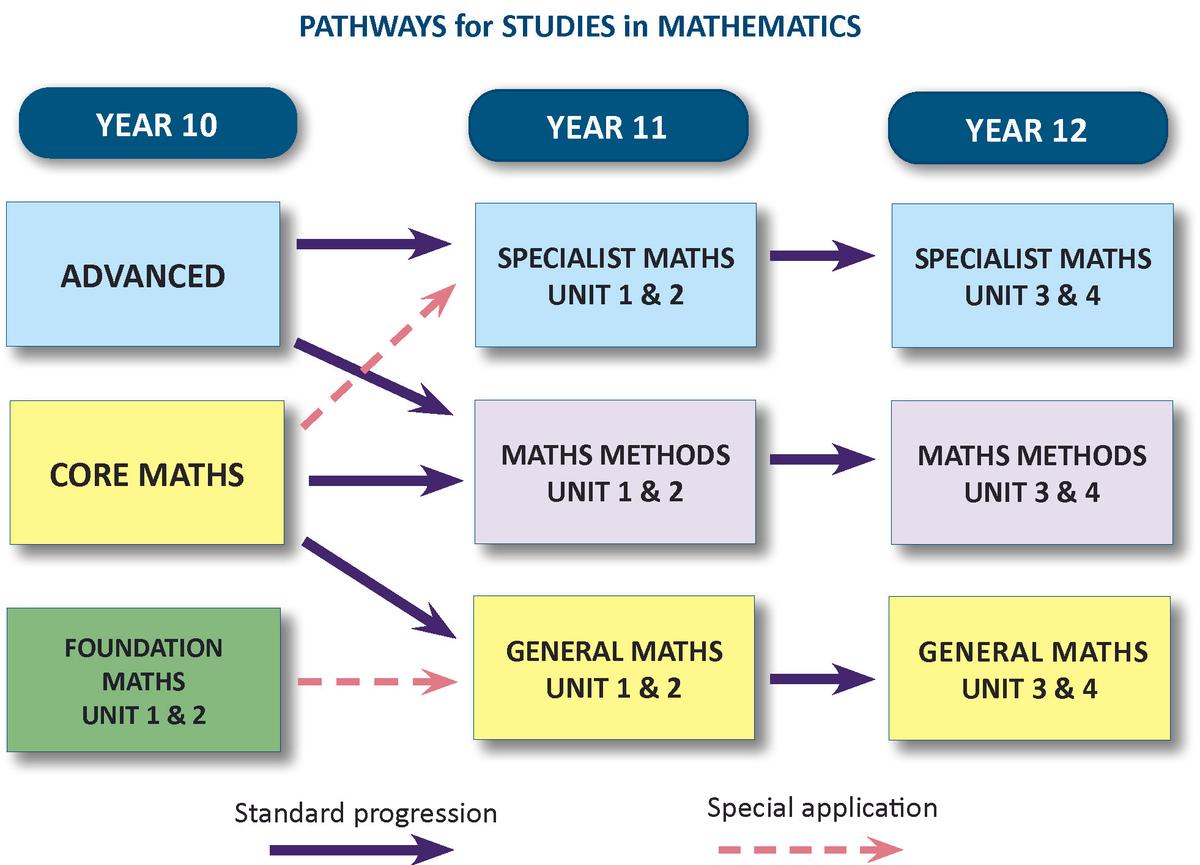
What Mathematics pathway should I choose in VCE?
The flowchart below shows the possible pathways for studying VCE Mathematics
Note: For VCE Mathematics Studies all Student Assessed Coursework (tests and tasks) and Examinations are set assuming students own or have access to an approved CAS calculator.
Examination 1 for both Mathematical Methods Units 3 & 4 and Specialist Mathematics Units 3&4 will be a 1 hour technology free (no calculator, no notes) examination.
Examination 2 for both Mathematical Methods Units 3 & 4 and Specialist Mathematics Units 3&4 will be a 2 hour technology-active (calculators and bound reference notes may be used) examination.
Examinations 1 and Examination 2 for General Mathematics Units 3 & 4 will be 90 minute technology-active (calculators and bound reference notes may be used) examinations.
Possible pathways for studies in Mathematics
VCE Foundation Mathematics
VCE Foundation Mathematics (Units 1 & 2) provides for the continuing development of students who need mathematical skills to support their other VCE subjects. Successful completion of Foundation Mathematics also satisfies the Numeracy component of the VCE Vocational Major.
VCE Foundation Mathematics has a strong emphasis on using mathematics in practical contexts relating to everyday life. Students are encouraged to use appropriate technology in all areas of their study. Success in this course of study enables only limited choice for students intending to study VCE General Mathematics (Units 1 & 2).
Foundation Mathematics Units 1 and 2 focus on providing students with the mathematical knowledge, skills, understanding and dispositions to solve problems in real contexts for a range of workplace, personal, further learning, and community settings relevant to contemporary society. Students are encouraged to use appropriate technology in all areas of their study.
The areas of study for Foundation Mathematics are:
- Algebra, number and structure
- Data analysis, probability and statistics
- Discrete mathematics
- Space and measurement
- Functions, relations and graphs
The award of satisfactory completion for a unit is based on whether the student has demonstrated achievement of the set of outcomes 1, 2 and 3 listed below. All assessments at Units 1 and 2 are school-based, are a part of the regular teaching and learning program, and completed mainly in class and within a limited timeframe. The decision will be based on the teacher’s assessment of the student’s overall performance on assessment tasks designated for the unit. Example assessment tasks include - Outcome 1: Assignments, summary or review notes, tests Outcome 2: A report on an application or use of mathematics, a presentation in oral, written, poster, or multimedia format Outcome 3: Effective and appropriate use of technology in contexts related to topics in the selected material from the areas of study.
Outcomes for satisfactory completion:
- to be able to use and apply a range of mathematical concepts, skills and procedures from selected areas of study to solve practical problems based on a range of everyday and real-life contexts.
- to apply mathematical processes in non-routine practical contexts, including situations with some open-ended aspects requiring investigative, modelling or problem-solving techniques or approaches, and analyse and discuss these applications of mathematics.
- to be able to apply computational thinking and use numerical, graphical, symbolic and statistical functionalities of technology to develop mathematical ideas, produce results and carry out analysis in practical situations requiring investigative, modelling or problem-solving techniques or approaches.