Year 8 Mathematics

Measurement and geometry

by Helen Kerr-Lawley, Maths Teacher

The Year 8 Mathematics class has continued to enjoy their mathematical learning in the current unit, Measurement and Geometry, discovering links between three-dimensional solids and networks. This is part of a branch of mathematics called topology which is used to solve real-world problems in such diverse areas as communications, public transport, computer programming, quantum physics, superconductivity and superfluids.

Students first created 3D solids (with or without their own added decorations) with choices between straightforward pentagonal & hexagonal prisms or pyramids, or more complicated shapes such as rhombic prisms, octahedrons, dodecahedrons and icosohedrons.

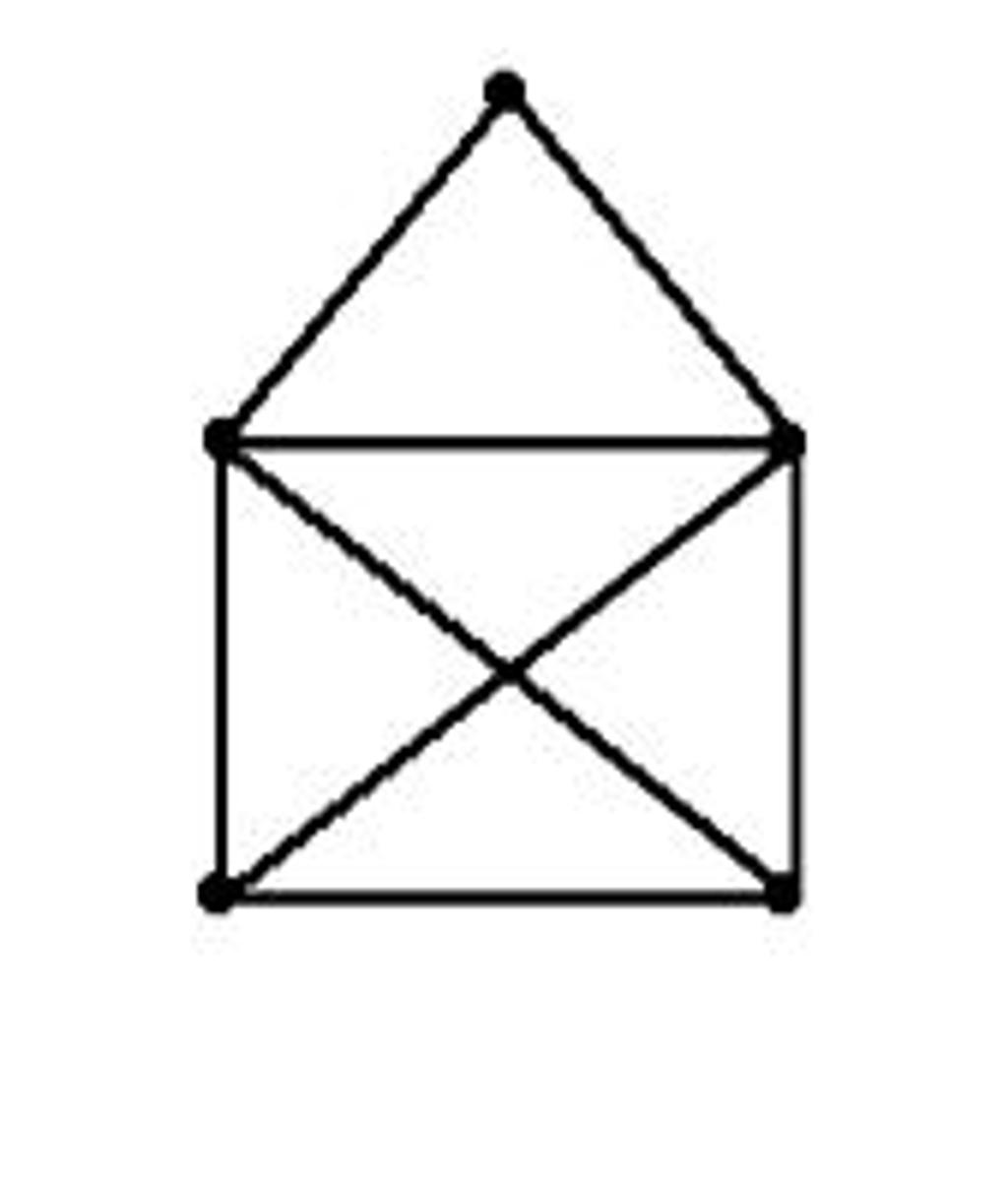
We then looked at networks which involved solving puzzles (like the one directly below) where the challenge is to trace a path for the whole network without going over a line twice and if you can, it means that you have an Euler Path.

The next puzzle was: Can you trace a path for the whole network shown below but start and finish at the same point? If so, then you have found an Euler Circuit!

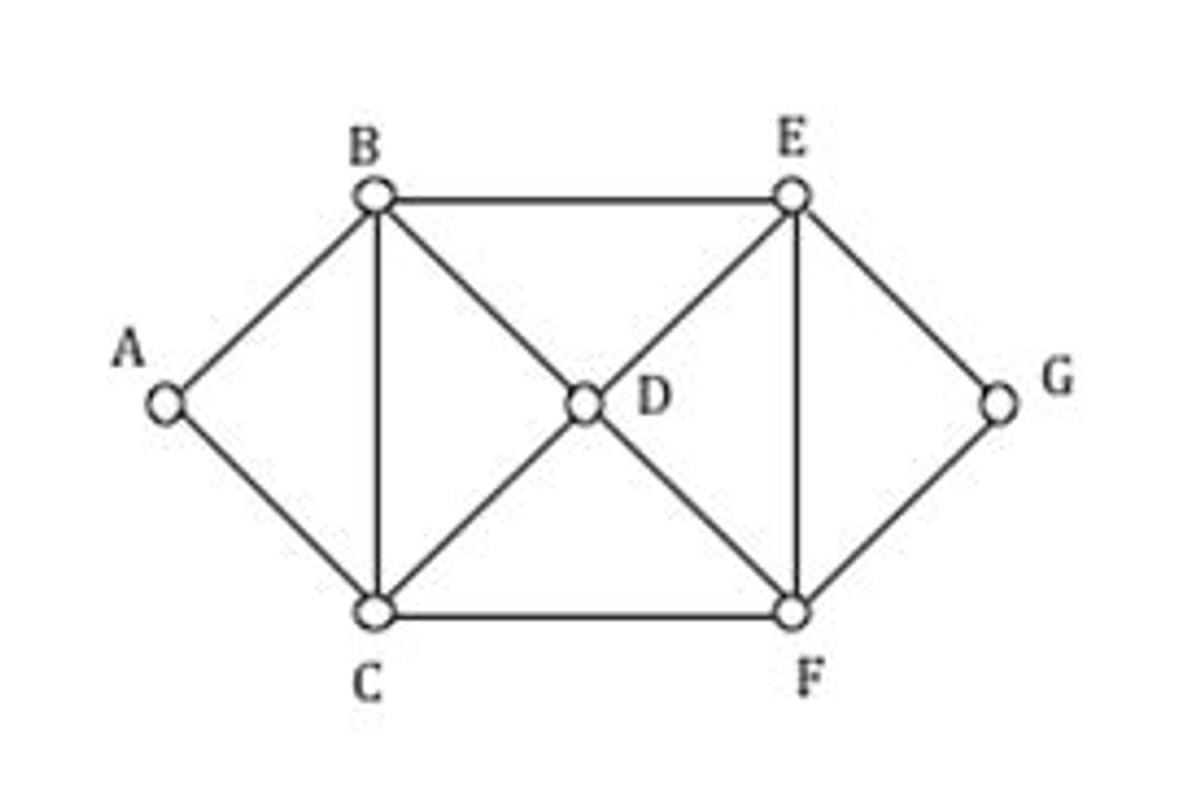
The students then made their own networks and counted the number of edges, vertices and regions to discover a simple mathematical relationship. We returned to the three-dimensional shapes to find that there is a mathematical relationship for the number of edges, faces and vertices too…and it is the same formula as the one for networks!

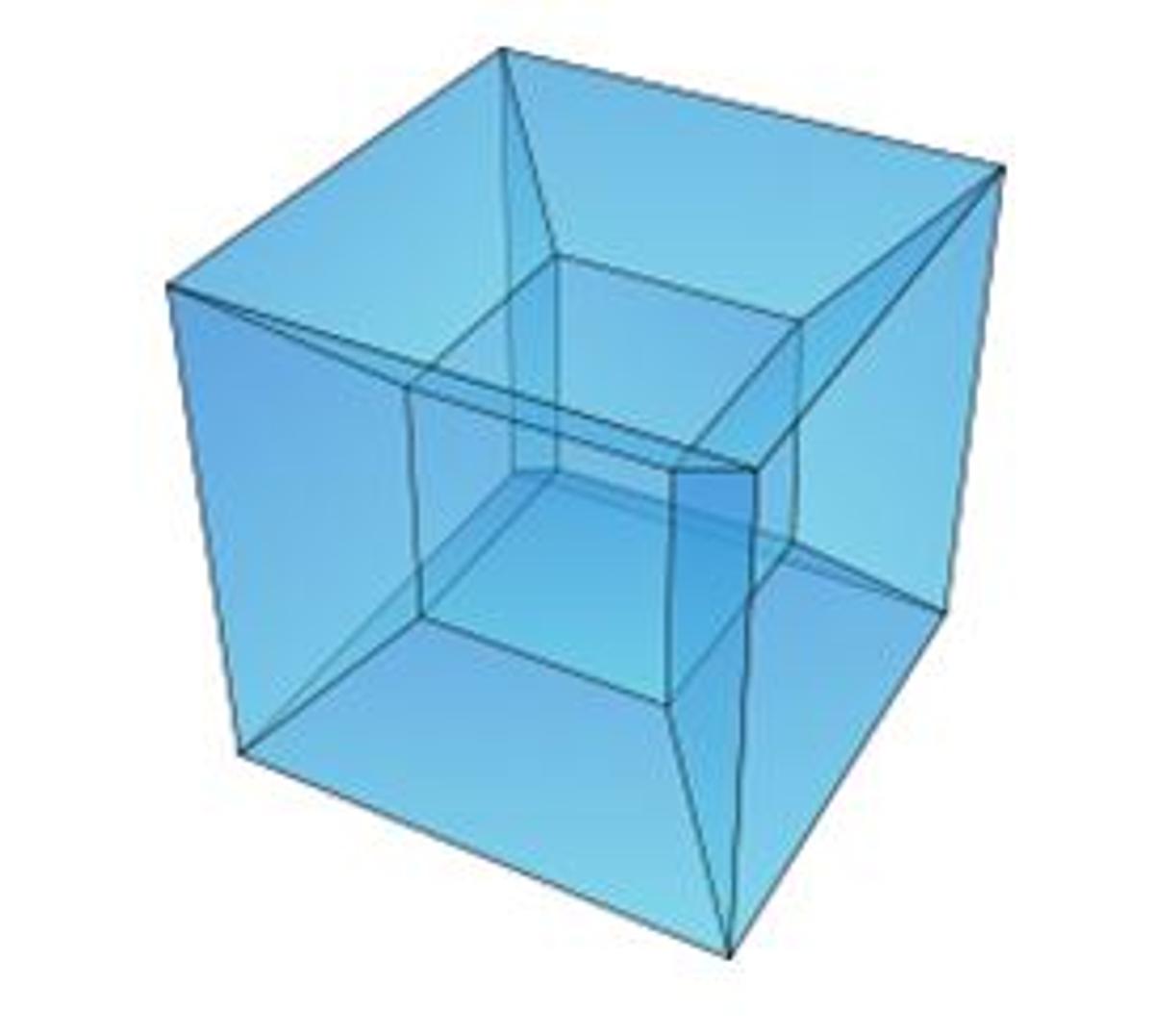
We also briefly discussed Graham’s number which was described as “the largest number used in a mathematical proof” (Gardiner, 1977) and is much bigger than a googol (10 to the power of 100) or googleplex (10 to the power of googol) and is used in explaining the connections between the vertices of a hypercube such as the one shown below.

We shall continue to ponder the wonders of geometry for the rest of the year!