Numeracy

Mathematics extension groups 2024

This year I’ve had the pleasure of working with 80 students from Prep to Year Four in a weekly extension program. Sessions gave these students opportunities to apply their number sense to a range of games and problem solving activities. While learning tasks were aimed to provide our students with challenge, they were also designed to deepen their understanding of working mathematically, with a strong emphasis on collaborating with others.

Each session began with a warm up involving games with cards, dominoes and dice. Students engaged in a range of number sense thinking from finding the largest sum, smallest difference or greatest product, to adding unit fractions with different denominators to find the amount closest to one. It was always great to see the students willing to challenge themselves in trying a game variation with a step up in its level of complexity. 

Here are just a few samples of the work our Mathematicians have been doing:

Prep – Year One group explored multiplication with the problem, ‘The product is 48, what could the question be?’ They used concrete materials to create arrays and investigate which whole numbers could be multiplied to make 48.

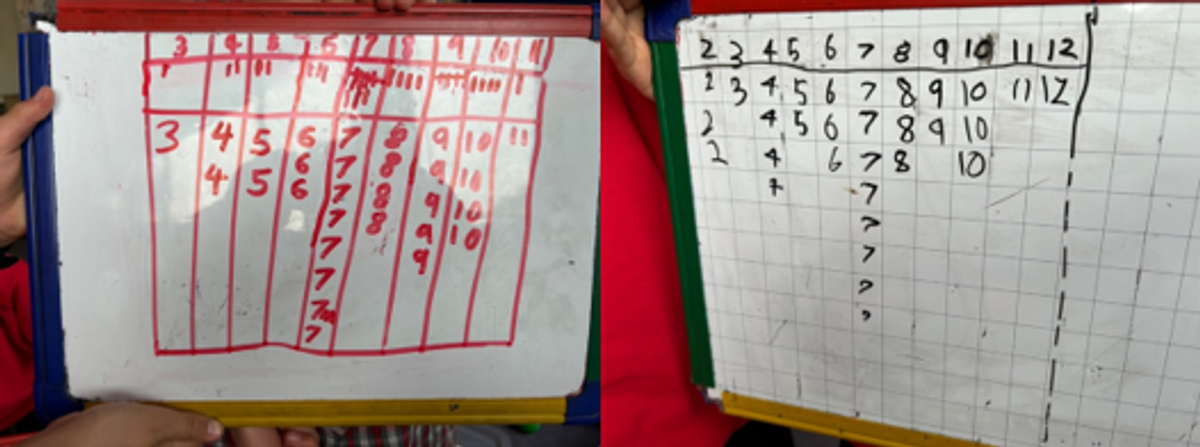
The Year Two and Three groups investigated the frequency of making the sums 2-12 when rolling 2 six-sided dice. They contributed to this experiment collating data in small groups before joining their findings together. We discussed terms mean, mode and median, and students discussed why some numbers were more likely to be rolled than others.

Year Three and Four groups were provided with a variety of problem solving prompts requiring students to consider tasks from different perspectives. Problems often involved trial and error, had multiple solutions and pathways to finding solutions, and were most successfully solved when students collaborated.

‘Move only three matchsticks to make 5 squares’

‘Work out all possible answers for this addition 2_6 + _8 = _2_’

Followed by a similar problem: 5_2 - _ _4 = 68

Students were able to build their ability to collaborate effectively with a variety of their peers, in random groups of three. They showed great willingness to share their thinking, try new ideas, explain and justify their solutions and be resilient and curious when the first step in tackling a problem was not initially obvious. Students demonstrated their capability to move through trial and error, to looking for patterns, to finding rules, to becoming increasingly systematic in their thinking and recording.

It has been wonderful working with so many learners within these extension groups. I look forward to seeing how they continue to apply their collaboration and skills working mathematically in our classroom programs.

Robyn Davis

Numeracy Leader