Maths Learning 

AREA!

Kathryn Dowling

Teacher - Mathematics

Measurement is pivotal in helping quantify the world around us.

To deepen their understanding of how to calculate the area of a shape, students must be given opportunities to investigate and develop problem-solving skills toward their learning goal. More often than not, practical tasks significantly help to cement mathematical concepts as students are able to visualise a given concept and test it on a practical basis (see photos of Ben and Emily's workbooks below). These activities allow students to draw on their existing maths knowledge and apply it to new situations, strengthening their mathematical skillset as they move through the process.

In this vein, students in Home Group 8S recently spent two lessons deriving area formulae of parallelograms, kites and trapezia, using their existing knowledge of rectangular area. 

Students learned how to derive the formula for the area of a circle by physically cutting up a circle and rearranging its wedges into a rectangle.  Emily, Patrick and Ben volunteered to share their work and understandings on behalf of the class. 

Emily Lynch

Year 8

We are learning about the area of a circle.  You can cut up a circle and make it into a rectangle shape, which will make it easier to find the formula to calculate the area.

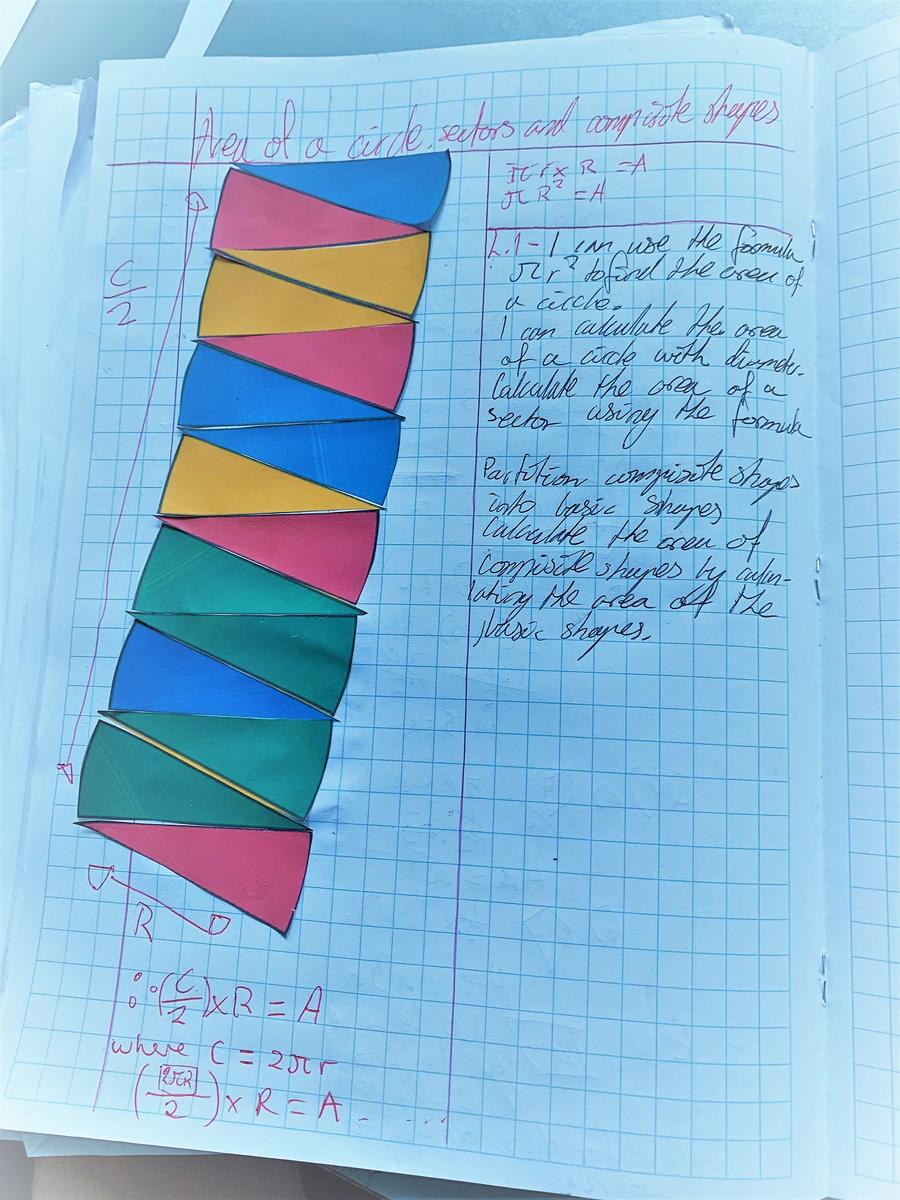
Ben Gillespie

Year 8

You take the sectors of a circle and form them into a rectangle. The theory is  that if you had infinite sectors, it would make a perfect rectangle.   The length is circumference over 2, and the width is r (the radius).   You can replace circumference with 2πr , which gives you an area formula of  πr squared.